
11. Exponents and Powers
Section outline
-
-
Solutions to Ex 11.1
Q1. Find the value of:
Ans:
(i) 26 = 2 x 2 x 2 x 2 x 2 x 2 = 64
(ii) 93 = 9 x 9 x 9 = 729
(iii) 112 = 11 x 11 = 121
(iv) 54 = 5 x 5 x 5 x 5 = 625
Q2. Express the following in exponential form:
Ans:
(i) 6 x 6 x 6 x 6 = 64
(ii) t x t = t2
(iii) b x b x b x b = b4
(iv) 5 x 5 x 7 x 7 x 7 = 52 x 73
(v) 2 x 2 x a x a = 22 x a2
(vi) a x a x a x c x c x c x c x d = a3 x c4 x d
Q3. Express each of the following numbers using exponential notation:
Ans:
(i) 512 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 29
(ii) 343 = 7 x 7 x 7 = 73
(iii) 729 = 3 x 3 x 3 x 3 x 3 x 3 = 36
(iv) 3125 = 5 x 5 x 5 x 5 x 5 = 55
Q4. Identify the greater number, wherever possible, in each of the following?
Ans:
(i) 43 or 34
43 = 4 x 4 x 4 = 64
34= 3 x 3 x 3 x 3 = 81
34 is the greater number.
(ii) 53 or 35
53 = 5 x 5 x 5 = 125
35= 3 x 3 x 3 x 3 x 3 = 243
35 is the greater number.
(iii) 28 or 82
28 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 256
82 =8 x 8 = 64
28 is the greater number.
(iv) 1002 or 2100
1002 = 100 x 100 = 10000
2100 = (1024)10
2100 is the greater number.
(v) 210 or 102
210 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2= 1024
102 = 10 x 10 = 100
210 is the greater number.
Q5. Express each of the following as product of powers of their prime factors:
Ans:
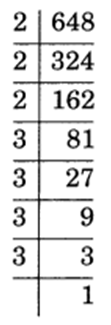
(i) 648 = 2 x 2 x 2 x 3 x 3 x 3 x 3 = 23 x 34
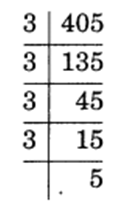
(ii) 405 = 3 x 3 x 3 x 3 x 5 = 34 x 5
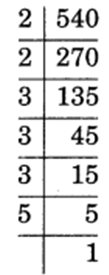
(iii) 540 = 2 x 2 x 3 x 3 x 3 x 5 = 22 x 33 x 5
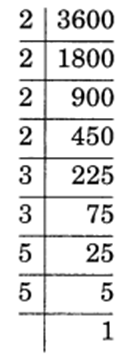
(iv) 3600 = 2 x 2 x 2 x 2 x 3 x 3 x 5 x 5 = 24 x 32 x 52
Q6. Simplify:
Ans:
(i) 2 x 103 = 2 x 10 x 10 x 10 = 2000
(ii) 72 x 22 = 7 x 7 x 2 x 2 = 196
(iii) 23 x 5 = 2 x 2 x 2 x 5 = 40
(iv) 3 x 44 = 3 x 4 x 4 x 4 x 4 = 768
(v) 0 x 102 = 0
(vi) 52 x 33 = 5 x 5 x 3 x 3 x 3 = 675
(vii) 24 x 32 = 2 x 2 x 2 x 3 x 3 = 144
(viii) 32 x 104 = 3 x 3 x 10 10 x 10 x 10 = 90000
Q7. Simplify:
Ans:
(i) (– 4)3 = (– 4) x (– 4) x (– 4) = – 64
(ii) (–3) x (–2)3 = (–3) x (–2) x (–2) x (–2) = 24
(iii) (–3)2 x (–5)2 = (–3) x (–3) x (–5) x (–5) = 225
(iv) (–2)3 x (–10)3 = (–2) x (–2) x (–2) x (–10) x (–10) x (–10) = 8000
Q8. Compare the following numbers:
Ans:
(i) 2.7 x 1012 ; 1.5 x 108
Comparing the exponents,
1012 > 108
Thus, 2.7 x 1012 > 1.5 x 108
(ii) 4 x 1014 ; 3 x 1017
Comparing the exponents,
1014< 1017
Thus, 4 x 1014 < 3 x 1017
-
Solutions to Ex. 11.2
Q1. Using laws of exponents, simplify and write the answer in exponential form:
Ans:
(i) 32 x 34 x 38 = 3(2 + 4 + 8) = 314
(ii) 615 ÷ 610 = 6(15 - 10) = 65
(iii) a3 x a2 = a(3 + 2) = a5
(iv) 7x x 72 = 7 x + 2
(v) (52)3 ÷ 53= 5(2 x 3) ÷ 53
= 5(6 - 3) = 53
(vi) 25 × 55 = (2 x 5)5 = 105
(vii) a4 × b4 = (ab)4
(viii) (34)3 = 3(4 x 3) = 312
(ix) (220 ÷ 215) x 23
= 2 (20 - 15) x 23
= 25 x 23 = 2 (5 = 3) = 28
(x) 8t ÷ 82 = 8t - 2
Q2. Simplify and express each of the following in exponential form:
Ans:
(i) \( \frac{2^3 \times 3^4 \times 4}{3 \times 32} \)
= \( \frac{2^3 \times 3^4 \times 2^2}{3 \times 2^5} \) = \( \frac{2^{3+2} \times 3^4}{3 \times 2^5} \)
= \( \frac{2^5 \times 3^4}{3 \times 2^5} \) = 3(4 - 1) = 33
(ii) ((52)3 x 54) ÷ 57 = (52 x 3 x 54) ÷ 57
= (56 x 54) ÷ 57 = (56 + 4 ) ÷ 5 = 510 ÷ 5
= 510 - 7 = 53
(iii) 254 ÷ 53 = (52)4 ÷ 53
= 52 × 4 ÷ 53 = 58 ÷ 53
= 58-3 = 55
(iv) \( \frac{3 \times 7^2 \times 11^8}{21 \times 11^3} \)
= \( \frac{3 \times 7^2 \times 11^8}{3 \times 7 \times 11^3} \)
= 72-1 x 118 – 3 = 7 x 115
(v) \( \frac{3^7}{3^4 \times 3^3} \) = ( \frac{3^7}{3^{4 +3}} \)
= \( \frac{3^7}{3^7} \) = 37 - 7 = 1 or 30
(vi) 20 + 30 + 40 = 1 + 1 + 1 = 3
(vii) 20 x 30 x 40 = 1 x 1 x 1 = 1
(viii) (30 + 20) × 50 = (1 + 1) x 1
= 2 x 1 = 1
(ix) \( \frac{2^8 \times a^5}{4^3 \times a^3} \)
As, (4)3 = (22)3 = 22 x 3 = 26
\( \frac{2^8 \times a^5}{4^3 \times a^3} \) = \( \frac{2^8 \times a^5}{2^6 \times a^3} \)
= 28 – 6 x a5 – 3 = 2a2
(x) (\( \frac{a^5}{a^3} \)) x a8
= (a5 -3) x a8 = a2 x a8
= a2 + 8 = a10
(xi) \( \frac{4^5 \times a^8 \times b^3}{4^5 \times a^5\times b^2} \)
= 45 – 5 x a8 – 5 x b3 – 2 = 40 x a3 x b
= a3b
(xii) (23 × 2)2 = (23 + 1)2
= (24)2 = 24 × 2 = 28
Q3. Say true or false and justify your answer:
Ans:
(i) 10 x 1011 = 10011
LHS = 10 x 1011= 101 + 11
LHS = 1012
RHS = 10011 = (102)11 = 102 x 11
RHS = 1022
As, 1012 ≠ 1022
The statement 10 x 1011 = 10011 is false.
(ii) 23 > 52
LHS = 23 = 2 x 2 x 2
LHS = 8
RHS = 52 = 5 x 5
RHS = 25
As, 8 ≠ 25
The statement 23 > 52 is false.
(iii) 23 x 32 = 65
LHS = 23 x 32 = 2 x 2 x 2 x 3 x 3
LHS = 72
RHS = 65 = 6 x 6 x 6 x 6 x 6
RHS = 7776
As, 72 ≠ 7776
The statement 23 x 32 = 65 is false.
(iv) 30 = (1000)0
LHS = 30 = 1
RHS = (1000)0 = 1
LHS = RHS
Thus, 30 = (1000)0 is true.
Q4. Express each of the following as a product of prime factors only in exponential form:
Ans:
(i) 108 × 192
Prime factors of 108 = 2 x 2 x 3 x 3 x 3 = 22 x 33
Prime factors of 192 = 2 x 2 x 2 x 2 x 2 x 2 x 3 = 26 x 3
Thus, 108 × 192 = (22 x 33) x (26 x 3)
= 22 + 6 x 33 + 1 = 28 x 34
(ii) 270 = 2 x 3 x 3 x 3 x 5 = 2 x 33 x 5
(iii) 729 × 64
Prime factors of 729 = 3 x 3 x 3 x 3 x 3 x 3 = 36
Prime factors of 64 = 2 x 2 x 2 x 2 x 2 x 2 = 26
Thus, 729 × 64 = 36 x 26
(iv) 768 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 3 = 28 x 3
Q5. Simplify:
Ans:
(i) \( \frac{({2^5})^2 \times 7^3}{8^3 \times 7} \)
= \( \frac{2^{(5 \times2)} \times 7^3}{({2^3})^3 \times 7} \)
= \( \frac{2^{10} \times 7^3}{2^9 \times 7} \) = 2(10-9) x 7(3-1)
= 2 x 72 = 2 x 7 x 7 = 98
(ii) \( \frac{25 \times 5^2 \times t^8}{10^3 \times t^4} \)
= \( \frac{5^2 \times 5^2 \times t^8}{{(5 \times 2)}^3 \times t^4} \)
= \( \frac{5^{2 + 2} \times t^8}{5^3 \times 2^3 \times t^4} \)
= \( \frac{5^{4 - 3} \times t^{8 - 4}}{2^3} \) = \( \frac{5t^4}{8} \)
(iii) \( \frac{3^5 \times 10^5 \times 25}{5^7 \times 6^5} \)
= \( \frac{3^5 \times {(5 \times 2)}^5 \times 5^2}{5^7 \times {(2 \times 3)}^5} \)
= \( \frac{3^5 \times 5^5 \times 2^5 \times 5^2}{5^7 \times 2^5 \times 3^5} \)
= 2(5 - 5) x 3(5 - 5) x 5(5 + 2 - 7) = 20 + 30 + 50 = 1
-
Solutions to Ex. 11.3
Q1. Write the following numbers in the expanded forms:
Ans:
(i) 279404
= 2 x 100000 + 7 x 10000 + 9 x 1000 + 4 x 100 + 0 x 10 + 4 x 1
= 2 x 105 + 7 x 104 + 9 x 103 + 4 x 102+ 4 x 100
(ii) 3006194
= 3 x 1000000 + 0 x 100000 + 0 x 10000 + 6 x 1000 + 1 x 100 + 9 x 10 + 4 x 1
= 3 x 106 + 6 x 103 + 1 x 102+ 9 x 101 + 4 x 100
(iii) 2806196
= 2 x 1000000 + 8 x 100000 + 0 x 10000 + 6 x 1000 + 1 x 100 + 9 x 10 + 6 x 1
= 2 x 105 + 8 x 104 + 6 x 103+ 1 x 102 + 9 x 101 + 6 x 100
(iv) 120719
= 1 x 100000 + 2 x 10000 + 0 x 1000 + 7 x 100 + 1 x 10 + 9 x 1
= 1 x 105 + 2 x 104 + 7 x 102+ 1 x 101 + 9 x 100
(v) 20068
= 2 x 10000 + 0 x 1000 + 0 x 100 + 6 x 10 + 8 x 1
= 2 x 104 + 6 x 101 + 8 x 100
Q2. Find the number from each of the following expanded forms:
Ans:
(a) (8 x 10)4 + (6 x 10)3 + (0 x 10)2 + (4 x 10)1 + (5 x 10)0
= (8 x 10000) + (6 x 1000) + (0 x 100) + (4 x 10) + (5 x 1)
= 80000 + 6000 + 0 + 40 + 5 = 86045
(b) (4 x 10)5 + (5 x 10)3 + (3 x 10)2 + (2 x 10)0
= (4 x 100000) + (0 x 10000) + (5 x 1000) + (3 x 100) + (0 x 10) + (2 x 1)
= 400000 + 0 + 5000 + 300 + 0 + 2 = 405302
(c) (3 x 10)4 + (7 x 10)2 + (5 x 10)0
= (3 x 10000) + (0 x 1000) + (7 x 100) + (0 x 10) + (5 x 1)
= 30000 + 0 + 700 + 0 + 5 = 30705
(d) (9 x 10)5 + (2 x 10)2 + (3 x 10)1
= (9 x 100000) + (0 x 10000) + (0 x 1000) + (2 x 100) + (3 x 10) + (0 x 1)
= 900000 + 0 + 0 + 200 + 30 + 0 = 900230
Q3. Express the following numbers in standard form:
Ans:
(i) 5,00,00,000 = 5 x 107
(ii) 70,00,000 = 7 x 106
(iii) 3,18,65,00,000 = 3.1865 x 109
(iv) 3,90,878 = 3.90878 x 105
(v) 39087.8 = 3.90878 x 104
(vi) 3908.78 = 3.90878 x 103
Q4. Express the number appearing in the following statements in standard form.
Ans:
(a) 384,000,000 m = 3.84 x 108m
(b) 300,000,000 m/s = 3 x 108m/s
(c) 1,27,56,000 m = 1.2756 x 107m
(d) 1,400,000,000 m = 1.4 x 109m
(e) 100,000,000,000 stars = 1 x 1011 stars
(f) 12,000,000,000 years = 1.2 x 1010
(g) 300,000,000,000,000,000,000 m = 3 x 1020m
(h) 60,230,000,000,000,000,000,000 molecules = 6.023 x 1022
(i) 1,353,000,000 cubic km = 1.353 x 109
(j) 1,027,000,000 = 1.027 x 109
-
