8. Rational Numbers

Solutions to Ex. 8.1

Q1. List five rational numbers between:

Ans:

(i) –1 and 0

-1 < \( \frac{-2}{3} \) < \( \frac{-3}{5} \) < \( \frac{-1}{2} \) < \( \frac{-2}{5} \) < \( \frac{-1}{5} \) < 0

Rational numbers between –1 and 0 are: \( \frac{-2}{3} \), \( \frac{-3}{5} \), \( \frac{-1}{2} \), \( \frac{-2}{5} \) & \( \frac{-1}{5} \).

(ii) –2 and –1

-2 < \( \frac{-5}{3} \) < \( \frac{-3}{2} \) < \( \frac{-6}{5} \) < \( \frac{-9}{8} \) < \( \frac{-12}{11} \) < -1

Rational numbers between –2 and -1 are: \( \frac{-5}{3} \), \( \frac{-3}{2} \), \( \frac{-6}{5} \), \( \frac{-9}{8} \) & \( \frac{-12}{11} \).

(iii) \( \frac{-4}{5} \) & \( \frac{-2}{3} \)

The LCM of both the denominators = 15

Thus, \( \frac{-4}{5} \) = \( \frac{-12}{15} \) &

\( \frac{-2}{3} \) = \( \frac{-10}{15} \)

Finding rational numbers between \( \frac{-12}{15} \) & \( \frac{-10}{15} \)

\( \frac{-12}{15} \) < \( \frac{-7}{9} \) < \( \frac{-34}{45} \) < \( \frac{-11}{15} \) < \( \frac{-32}{45} \) < \( \frac{-31}{45} \) < \( \frac{-10}{15} \)

Rational numbers between \( \frac{-4}{5} \) & \( \frac{-2}{3} \) are: \( \frac{-7}{9} \), \( \frac{-34}{45} \), \( \frac{-11}{15} \), \( \frac{-32}{45} \) & \( \frac{-31}{45} \)

(iv) \( \frac{-1}{2} \) & \( \frac{2}{3} \)  

\( \frac{-1}{2} \) < \( \frac{-1}{3} \) < \( \frac{-1}{4} \) < 0 \( \frac{1}{3} \)< \( \frac{1}{2} \) < \( \frac{2}{3} \)  

Rational numbers between \( \frac{-1}{2} \) & \( \frac{2}{3} \)  are: \( \frac{-1}{3} \), \( \frac{-1}{4} \), 0, \( \frac{1}{3} \) & \( \frac{1}{2} \)

Q2. Write four more rational numbers in each of the following patterns:

Ans:

(i) \( \frac{-3}{5} \), \( \frac{-6}{10} \), \( \frac{-9}{15} \), \( \frac{-12}{20} \)

\( \frac{-6}{10} \) = \( \frac{-3 \times 2}{5 \times 2} \), \( \frac{-9}{15} \) = \( \frac{-3 \times 3}{5 \times 3} \) & \( \frac{-12}{20} \) = \( \frac{-3 \times 4}{5 \times 4} \)

Continuing the pattern, \( \frac{-3 \times 5}{5 \times 5} \) = \( \frac{-15}{25} \), \( \frac{-3 \times 6}{5 \times 6} \) = \( \frac{-18}{30} \), \( \frac{-3 \times 7}{5 \times 7} \) = \( \frac{-21}{35} \) & \( \frac{-3 \times 8}{5 \times 8} \) = \( \frac{-24}{40} \)

Thus, next four rational numbers are: \( \frac{-15}{25} \), \( \frac{-18}{30} \), \( \frac{-21}{35} \), \( \frac{-24}{40} \)

(ii) \( \frac{-1}{4} \), \( \frac{-2}{8} \), \( \frac{-3}{12} \)

\( \frac{-2}{8} \) = \( \frac{-1 \times 2}{4 \times 2} \), \( \frac{-3}{12} \) = \( \frac{-1 \times 3}{4 \times 3} \) 

Continuing the pattern, \( \frac{-1 \times 4}{4 \times 4} \) = \( \frac{-4}{16} \), \( \frac{-1 \times 5}{4 \times 5} \) = \( \frac{-5}{20} \), \( \frac{-1 \times 6}{4 \times 6} \) = \( \frac{-6}{24} \) & \( \frac{-1 \times 7}{4 \times 7} \) = \( \frac{-7}{28} \)

Thus, next four rational numbers are: \( \frac{-4}{16} \), \( \frac{-5}{20} \), \( \frac{-6}{24} \), \( \frac{-7}{28} \)

(iii) \( \frac{-1}{6} \), \( \frac{2}{-12} \), \( \frac{3}{-18} \), \( \frac{4}{-24} \)

\( \frac{2}{-12} \) = \( \frac{-1 \times -2}{6 \times -2} \),  \( \frac{3}{-18} \) = \( \frac{-1 \times -3}{6 \times -3} \) & \( \frac{4}{-24} \) = \( \frac{-1 \times -4}{6 \times -4} \) 

Continuing the pattern, \( \frac{-1 \times -5}{6 \times -5} \) = \( \frac{5}{-30} \), \( \frac{-1 \times -6}{6 \times -6} \) = \( \frac{6}{-36} \), \( \frac{-1 \times -7}{6\times -7} \) = \( \frac{7}{-42} \) & \( \frac{-1 \times -8}{6 \times -8} \) = \( \frac{8}{-48} \)

Thus, next four rational numbers are: \( \frac{5}{-30} \), \( \frac{6}{-36} \), \( \frac{7}{-42} \), \( \frac{8}{-48} \)

(iv) \( \frac{-2}{3} \), \( \frac{2}{-3} \), \( \frac{4}{-6} \), \( \frac{6}{-9} \)

\( \frac{2}{-3} \) = \( \frac{-2 \times -1}{3 \times -1} \), \( \frac{4}{-6} \) = \( \frac{-2\times -2}{3 \times -2} \) & \( \frac{6}{-9} \) = \( \frac{-2 \times -3}{3 \times -3} \)

Continuing the pattern, \( \frac{-2 \times -4}{3 \times -4} \) = \( \frac{8}{-12} \), \( \frac{-2 \times -5}{3 \times -5} \) = \( \frac{10}{-15} \), \( \frac{-2 \times -6}{3 \times -6} \) = \( \frac{12}{-18} \) & \( \frac{-2 \times -7}{3 \times -7} \) = \( \frac{14}{-21} \)

Thus, next four rational numbers are: \( \frac{8}{-12} \), \( \frac{10}{-15} \), \( \frac{12}{-18} \), \( \frac{14}{-21} \)

Q3. Give four rational numbers equivalent to:

Ans:

(i) \( \frac{-2}{7} \)

Four rational numbers are:

= \( \frac{-2 \times 2}{7 \times 2} \), \( \frac{-2 \times 3}{7 \times 3} \), \( \frac{-2 \times 4}{7 \times 4} \) & \( \frac{-2 \times 5}{7 \times 5} \), 

= \( \frac{-4}{14} \), \( \frac{-6}{21} \), \( \frac{-8}{28} \) & \( \frac{-10}{35} \)

(ii) \( \frac{5}{-3} \)

Four rational numbers are:

= \( \frac{5 \times 2}{-3 \times 2} \), \( \frac{5 \times 3}{-3 \times 3} \), \( \frac{5 \times 4}{-3 \times 4} \) & \( \frac{5 \times 5}{-3 \times 5} \)

= \( \frac{10}{-6} \), \( \frac{15}{-9} \), \( \frac{20}{-12} \) &\( \frac{25}{-15} \)

(iii) \( \frac{4}{9} \)

Four rational numbers are:

= \( \frac{4 \times 2}{9 \times 2} \), \( \frac{4 \times 3}{9 \times 3} \), \( \frac{4 \times 4}{9 \times 4} \) & \( \frac{4 \times 5}{9 \times 5} \)

= \( \frac{8}{18} \), \( \frac{12}{27} \), \( \frac{16}{36} \) & \( \frac{20}{45} \)

Q4. Draw the number line and represent the following rational numbers on it:

Ans:

(i) 

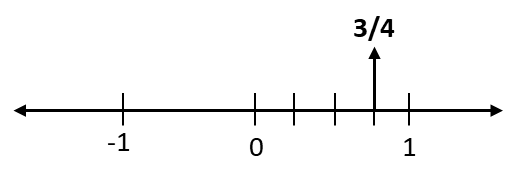
(ii)

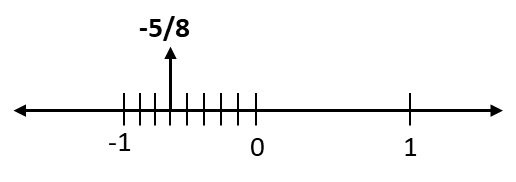
(iii)

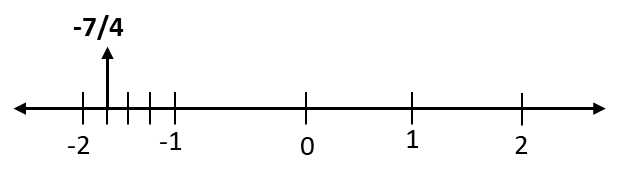
(iv)

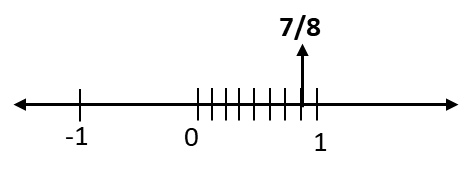
Q5. The points P, Q, R, S, T, U, A and B on the number line are such that, TR = RS = SU and AP = PQ = QB. Name the rational numbers represented by P, Q, R and S.

Ans:

A to B is divided into 3 equal parts.

Ap = PQ = QB = \( \frac{1}{3} \)

P = 2 + \( \frac{1}{3} \) = \( \frac{6 +1}{3} \)

P = \( \frac{7}{3} \)

Q = 2 + \( \frac{2}{3} \) = \( \frac{6 +2}{3} \)

Q = \( \frac{8}{3} \)

T to U is divided into 3 parts.

TR = RS = SU = \( \frac{1}{3} \)

R = -1 + \( \frac{-1}{3} \) = \( \frac{-3-1}{3} \)

R = \( \frac{-4}{3} \)

S = -1 + \( \frac{-2}{3} \) = \( \frac{-3-2}{3} \)

S = \( \frac{-5}{3} \)

Q6. Which of the following pairs represent the same rational number?

Ans:

(i) \( \frac{-7}{21} \) & \( \frac{3}{9} \)

Reducing the rational numbers to simplest form

\( \frac{-7}{21} \) = \( \frac{-1}{3} \)

\( \frac{3}{9} \) = \( \frac{1}{3} \)

\( \frac{-1}{3} \) \( \neq \) \( \frac{1}{3} \)

\( \frac{-7}{21} \) & \( \frac{3}{9} \) are not pairs.

(ii) \( \frac{-16}{20} \) & \( \frac{20}{-25} \)

Reducing the rational numbers to simplest form

\( \frac{-16}{20} \) = \( \frac{-4}{5} \)

\( \frac{20}{-25} \) = \( \frac{-4}{5} \)

\( \frac{-4}{5} \) = \( \frac{-4}{5} \)

\( \frac{-16}{20} \) & \( \frac{20}{-25} \) are pairs.

(iii) \( \frac{-2}{-3} \) & \( \frac{2}{3} \)

As, \( \frac{-2}{-3} \) = \( \frac{2}{3} \)

\( \frac{2}{3} \) = \( \frac{2}{3} \)

\( \frac{-2}{-3} \) & \( \frac{2}{3} \) are pairs.

(iv) \( \frac{-3}{5} \) & \( \frac{-12}{20} \)

Reducing the rational number to simplest form

\( \frac{-12}{20} \) = \( \frac{-3}{5} \)

\( \frac{-3}{5} \) = \( \frac{-3}{5} \)

\( \frac{-3}{5} \) & \( \frac{-12}{20} \) are pairs.

(v) \( \frac{8}{-5} \) & \( \frac{-24}{15} \)

Reducing the rational numbers to simplest form

\( \frac{8}{-5} \) = \( \frac{-8}{5} \)

\( \frac{-24}{15} \) = \( \frac{-8}{5} \)

\( \frac{-8}{5} \) = \( \frac{-8}{5} \)

\( \frac{8}{-5} \) & \( \frac{-24}{15} \) are pairs.

(vi) \( \frac{1}{3} \) & \( \frac{-1}{9} \)

As, \( \frac{1}{3} \) \( \neq \) \( \frac{-1}{9} \)

\( \frac{1}{3} \) & \( \frac{-1}{9} \) are not pairs.

(vii) \( \frac{-5}{-9} \) & \( \frac{5}{-9} \)

As, \( \frac{-5}{-9} \) = \( \frac{5}{9} \)

\( \frac{5}{9} \) \( \neq \) \( \frac{5}{-9} \)

\( \frac{-5}{-9} \) & \( \frac{5}{-9} \) are not pairs.

Q7. Rewrite the following rational numbers in the simplest form:

Ans:

(i) \( \frac{-8}{6} \)

\( \frac{-8 \div 2 }{6 \div 2 } \) = \( \frac{-4}{3} \)

(ii) \( \frac{25}{45} \)

\( \frac{25 \div 5 }{45 \div 5 } \) = \( \frac{5}{9} \)

(iii) \( \frac{-44}{72} \)

\( \frac{-44 \div 4 }{72 \div 4 } \) = \( \frac{-11}{18} \)

(iv) \( \frac{-8}{10} \)

\( \frac{-8 \div 2 }{10 \div 2 } \) = \( \frac{-4}{5} \)

Q8. Fill in the boxes with the correct symbol out of >, <, and =.

Ans:

(i) \( \frac{-5}{7} \) & \( \frac{2}{3} \)

LCM of the denominators is 21.

\( \frac{-5 \times 3}{7 \times 3} \) = \( \frac{-15}{21} \)

\( \frac{2 \times 7}{3 \times 7} \) = \( \frac{14}{21} \)

Comparing numerators, -15 < 14

Thus,\( \frac{-5}{7} \) < \( \frac{2}{3} \)

(ii) \( \frac{-4}{5} \) & \( \frac{-5}{7} \)

LCM of the denominators is 35.

\( \frac{-4 \times 7}{5 \times 7} \) = \( \frac{-28}{35} \)

\( \frac{-5 \times 5}{7 \times 5} \) = \( \frac{-25}{35} \)

Comparing numerators, -28 < -25

Thus, \( \frac{-4}{5} \) < \( \frac{-5}{7} \) 

(iii) \( \frac{-7}{8} \) & \( \frac{14}{-16} \)

Reducing \( \frac{14}{-16} \) to simplest form =  \( \frac{-7}{8} \)

Thus, \( \frac{-7}{8} \) =  \( \frac{-5}{7} \) 

(iv) \( \frac{-8}{5} \) & \( \frac{-7}{4} \)

LCM of the denominators is 20.

\( \frac{-8 \times 4}{5 \times 4} \) = \( \frac{-32}{20} \)

\( \frac{-7 \times 5}{4 \times 5} \) = \( \frac{-35}{20} \)

Comparing numerators, -32 > -35

Thus, \( \frac{-8}{5} \) > \( \frac{-7}{4} \)

(v) \( \frac{1}{-3} \) & \( \frac{-1}{4} \)

LCM of the denominators is 12.

\( \frac{1 \times -4}{-3 \times -4} \) = \( \frac{-4}{12} \)

\( \frac{-1 \times 3}{4 \times 3} \) = \( \frac{-3}{12} \)

Comparing numerators, -4 < -3

\( \frac{1}{-3} \) < \( \frac{-1}{4} \)

(vi) \( \frac{5}{-11} \) & \( \frac{-5}{11} \)

\( \frac{5}{-11} \) = \( \frac{-5}{11} \)

(vii) 0 & \( \frac{-7}{6} \)

0 > \( \frac{-7}{6} \)

(* Since 0 is greater than any negative rational number)

Q9. Which is greater in each of the following:

Ans:

(i) \( \frac{2}{3} \) & \( \frac{5}{2} \)

LCM of the denominators is 6.

\( \frac{2 \times 2}{3 \times 2} \) = \( \frac{4}{6} \)

\( \frac{5 \times 3}{2 \times 3} \) = \( \frac{15}{6} \)

Comparing numerators, 4 < 15

Thus, \( \frac{5}{2} \) is greater.

(ii) \( \frac{-5}{6} \) & \( \frac{-4}{3} \)

\( \frac{-4 \times 2}{3 \times 2} \) = \( \frac{-8}{6} \)

Comparing numerators, -5 > -8

Thus, \( \frac{-5}{6} \) is greater.

(iii) \( \frac{-3}{4} \) & \( \frac{2}{-3} \)

LCM of the denominators is 12.

 \( \frac{-3 \times 3}{4 \times 3} \) = \( \frac{-9}{12} \)

\( \frac{-2 \times 4}{3 \times 4} \) = \( \frac{-8}{12} \)

Comparing numerators, -9 < -8

Thus, \( \frac{2}{-3} \) is greater.

(iv) \( \frac{-1}{4} \), \( \frac{1}{4} \)

As denominators are same, comparing numerators

-1 < 1

Thus, \( \frac{1}{4} \) is greater.

(v) \( -3\frac{2}{7} \) & \( -3\frac{4}{5} \)

\( -3\frac{2}{7} \) = \( \frac{-23}{7} \) & \( -3\frac{4}{5} \) = \( \frac{-19}{5} \)

LCM of the denominators is 35.

\( \frac{-23 \times 5}{7 \times 5} \) = \( \frac{-115}{35} \)

\( \frac{-19 \times 7}{5 \times 7} \) = \( \frac{-133}{35} \)

Comparing numerators, -115 > -133

Thus, \( -3\frac{2}{7} \) is greater.

Q10. Write the following rational numbers in ascending order:

Ans:

(i)  \( \frac{-3}{5} \), \( \frac{-2}{5} \), \( \frac{-1}{5} \)

As denominators are same, comparing numerators

-3 < -2 < -1

Hence, ascending order is \( \frac{-3}{5} \), \( \frac{-2}{5} \), \( \frac{-1}{5} \).

(ii) \( \frac{-1}{3} \), \( \frac{-2}{9} \), \( \frac{-4}{3} \)

LCM of the denominators is 9.

\( \frac{-1 \times 3}{3 \times 3} \) = \( \frac{-3}{9} \)

\( \frac{-4 \times 3}{3 \times 3} \) = \( \frac{-12}{9} \)

Comparing numerators,

-12 < -3 < -2

Hence, ascending order is \( \frac{-4}{3} \),  \( \frac{-1}{3} \), \( \frac{-2}{9} \).

(iii) 

\( \frac{-3}{7} \), \( \frac{-3}{2} \), \( \frac{-3}{4} \)

LCM of the denominators is 28.

\( \frac{-3 \times 4}{7 \times 4} \) = \( \frac{-12}{28} \)

\( \frac{-3 \times 14}{2 \times 14} \) = \( \frac{-42}{28} \)

\( \frac{-3 \times 7}{4 \times 7} \) = \( \frac{-21}{28} \)

Comparing numerators,

-42 < -21 < -12

Hence, ascending order is \( \frac{-3}{2} \), \( \frac{-3}{4} \), \( \frac{-3}{7} \).

Solutions to Ex. 8.2

Q1. Find the sum:

Ans:

(i) \( \frac{5}{4} \) + \( \frac{-11}{4} \)

= \( \frac{5 - 11}{4} \) = \( \frac{-6}{4} \)

= \( \frac{-3}{2} \)  (Reducing to simple form)

(ii) \( \frac{5}{3} \) + \( \frac{3}{5} \)

LCM of 3 & 5 = 15

So, \( \frac{5}{3} \) = \( \frac{5 \times 5}{3 \times 5} \) = \( \frac{25}{15} \)

\( \frac{3}{5} \) = \( \frac{3 \times 3}{5 \times 3} \) = \( \frac{9}{15} \)

Thus, \( \frac{25}{15} \) + \( \frac{9}{15} \)

= \( \frac{34}{15} \)

(iii) \( \frac{-9}{10} \) + \( \frac{22}{15} \)

LCM of 10 & 15 is 30.

So,  \( \frac{-9}{10} \) =  \( \frac{-9 \times 3}{10 \times 3} \) = \( \frac{-27}{30} \)

\( \frac{22}{15} \) = \( \frac{22 \times 2}{15 \times 2} \) = \( \frac{44}{30} \)

Thus, \( \frac{-27}{30} \) + \( \frac{44}{30} \) = \( \frac{-27 + 44}{30} \)

= \( \frac{17}{30} \)

(iv) \( \frac{-3}{-11} \) + \( \frac{5}{9} \)

LCM of 11 & 9 is 99.

So, \( \frac{-3}{-11} \) = \( \frac{-3 \times 9}{-11 \times 9} \) = \( \frac{27}{99} \)

\( \frac{5}{9} \) = \( \frac{5 \times 11}{9 \times 11} \) = \( \frac{55}{99} \)

Thus, \( \frac{27}{99} \) + \( \frac{55}{99} \) 

= \( \frac{82}{99} \)

(v) \( \frac{-8}{19} \) + \( \frac{(-2)}{57} \)

LCM of 19 & 57 is 57.

So,  \( \frac{-8}{19} \) =  \( \frac{-8 \times 3}{19 \times 3} \) = \( \frac{-24}{57} \)

\( \frac{-24}{57} \) + \( \frac{(-2)}{57} \) = \( \frac{-24 + (-2)}{57} \)

= \( \frac{-26}{57} \)

(vi)  \( \frac{-2}{3} \) + 0 = \( \frac{-2}{3} \)

(vii) \( -2\frac{1}{3} \) + \( 4\frac{3}{5} \)

= \( \frac{-7}{3} \) + \( \frac{23}{5} \)

LCM of 3 & 5 = 15

So, \( \frac{-7}{3} \) = \( \frac{-7 \times 5}{3 \times 5} \) = \( \frac{-35}{15} \)

\( \frac{23}{5} \) = \( \frac{23 \times 3}{5 \times 3} \) = \( \frac{69}{15} \)

Thus, \( \frac{-35}{15} \) + \( \frac{69}{15} \) = \( \frac{-35 + 69}{15} \)

= \( \frac{34}{15} \)

Q2. Find

Ans:

(i) \( \frac{7}{24} \) - \( \frac{17}{36} \)

LCM of 24 & 36 is 72.

So, \( \frac{7}{24} \) = \( \frac{7 \times 3}{24 \times 3} \) = \( \frac{21}{72} \)

\( \frac{17}{36} \) = \( \frac{17 \times 2}{36 \times 2} \) = \( \frac{34}{72} \)

Thus, \( \frac{21}{72} \) - \( \frac{34}{72} \) = \( \frac{21 - 34}{72} \)

= \( \frac{-13}{72} \)

(ii) \( \frac{5}{63} \) - \( \frac{(-6)}{21} \)

LCM of 63 & 21 is 63.

So, \( \frac{(-6)}{21} \) = \( \frac{(-6 \times 3)}{21 \times 3} \) = \( \frac{-18}{63} \)

Thus, \( \frac{5}{63} \) - \( \frac{(-18)}{63} \) = \( \frac{5 + 18}{63} \)

= \( \frac{23}{63} \)

(iii) \( \frac{-6}{13} \) - \( \frac{(-7)}{15} \)

LCM of 13 & 15 is 195.

So, \( \frac{-6}{13} \) = \( \frac{-6 \times 15}{13 \times 15} \) = \( \frac{-90}{195} \)

\( \frac{-7}{15} \) = \( \frac{-7 \times 13}{15 \times 13} \) = \( \frac{-91}{195} \)

Thus, \( \frac{-90}{195} \) - \( \frac{(-91)}{195} \) = \( \frac{-90 + 91}{195} \)

= \( \frac{1}{195} \)

(iv) \( \frac{-3}{8} \) - \( \frac{(7)}{11} \)

LCM of 8 & 11 is 88.

So, \( \frac{-3}{8} \) = \( \frac{-3 \times 11}{8 \times 11} \) = \( \frac{-33}{88} \)

\( \frac{(7)}{11} \) = \( \frac{(7 \times 8)}{11 \times 8} \) = \( \frac{56}{88} \)

Thus, \( \frac{-33}{88} \) - \( \frac{56}{88} \) = \( \frac{-33 - 56}{88} \)

= \( \frac{-89}{88} \)

(v) \( -2\frac{1}{9} \) - 6

So, \( -2\frac{1}{9} \) = \( \frac{-19}{9} \)

& \( \frac{6 \times 9 }{1 \times 9} \) = \( \frac{54}{9} \)

Thus, \( \frac{-19}{9} \) - \( \frac{54}{9} \) = \( \frac{-19 - 54}{9} \)

= \( \frac{-73}{9} \)

Q3. Find the product:

Ans:

(i) \( \frac{9}{2} \) X \( \frac{-7}{4} \)

= product of numerators / product of denominators, 

= \( \frac{9 \times (-7)}{2 \times 4} \)

= \( \frac{-63}{8} \)

(ii) \( \frac{(3)}{10} \) X (-9)

= product of numerators / product of denominators, 

= \( \frac{3 \times (-9)}{10 \times 1} \)

= \( \frac{-27}{10} \)

(iii) \( \frac{-6}{5} \) X \( \frac{9}{11} \)

= product of numerators / product of denominators, 

= \( \frac{-6 \times 9}{5 \times 11} \)

= \( \frac{-54}{55} \)

(iv) 

\( \frac{3}{7} \) X \( \frac{(-2)}{5} \)

= product of numerators / product of denominators, 

= \( \frac{3 \times (-2)}{7 \times 5} \)

= \( \frac{-6}{35} \)

(v) \( \frac{9}{2} \) X \( \frac{(-7)}{4} \)

= product of numerators / product of denominators, 

= \( \frac{9 \times (-7)}{2 \times 4} \)

= \( \frac{-63}{8} \)

(vi) \( \frac{3}{(-5)} \) X \( \frac{(-5)}{3} \)

= product of numerators / product of denominators, 

= \( \frac{3 \times (-5)}{-5 \times 3} \)

= 1

Q4. Find the value of:

Ans:

(i) (-4) \( \div \) \( \frac{2}{3} \)

Reciprocal of \( \frac{2}{3} \) = \( \frac{3}{2} \)

So, (-4) X \( \frac{3}{2} \) = \( \frac{(-4) \times 3}{2} \)

= -6

(ii) \( \frac{-3}{5} \) \( \div \) 2

Reciprocal of 2 = \( \frac{1}{2} \)

So,  \( \frac{-3}{5} \) X \( \frac{1}{2} \) = \( \frac{-3 \times 1}{2 \times 5} \)

= \( \frac{-3}{10} \)

(iii) \( \frac{-4}{5} \) \( \div \) (-3)

Reciprocal of (-3) = \( \frac{-1}{3} \)

So,  \( \frac{-4}{5} \) X \( \frac{-1}{3} \) = \( \frac{-4 \times (-1)}{5 \times 3} \)

= \( \frac{4}{15} \)

(iv) \( \frac{-1}{8} \) \( \div \) \( \frac{3}{4} \)

Reciprocal of \( \frac{3}{4} \) = \( \frac{4}{3} \)

So, \( \frac{-1}{8} \) X \( \frac{4}{3} \) = \( \frac{-1 \times 4}{8 \times 3} \)

= \( \frac{-1}{6} \)

(v) \( \frac{-2}{13} \) \( \div \) \( \frac{1}{7} \)

Reciprocal of \( \frac{1}{7} \) = 7

So, \( \frac{-2}{13} \) X 7 = \( \frac{-2 \times 7}{13} \)

= \( \frac{-14}{13} \)

(vi) \( \frac{-7}{12} \) \( \div \) \( \frac{-2}{13} \)

Reciprocal of \( \frac{-2}{13} \) = \( \frac{-13}{2} \)

So, \( \frac{-7}{12} \) X \( \frac{-13}{2} \) = \( \frac{-7 \times (-13)}{12 \times 2} \)

= \( \frac{91}{24} \)

(vii) \( \frac{3}{13} \) \( \div \) \( \frac{-4}{65} \)

Reciprocal of \( \frac{-4}{65} \) = \( \frac{-65}{4} \)

So, \( \frac{3}{13} \) X \( \frac{-65}{4} \) = \( \frac{3 \times (-65)}{13 \times 4} \)

= \( \frac{-15}{4} \)