2. Fractions and Decimals

Solutions to Ex. 2.1

Q1. Which of the drawings (a) to (d) show:

Ans:

(i) 2 x 1/5: (d)

(ii) 2 x 1/2: (b)

(iii) 3 x 2/3: (a)

(iv) 3 x 1/4: (c)

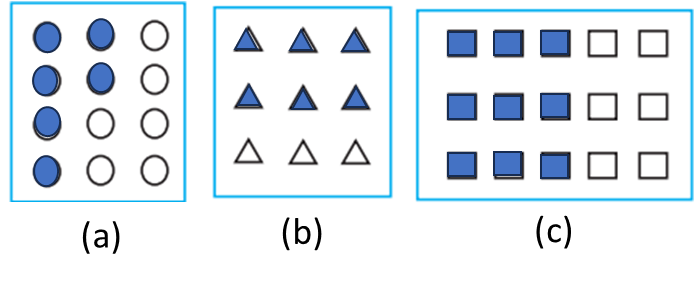
Q2. Some pictures (a) to (c) are given below. Tell which of them show:

Ans:

(i) 3 x 1/5 = 3/5 : (c)

(ii) 2 x 1/3 = 2/3 : (a)

(iii) 3 x 3/4 = \(2\frac{1}{4}\) : (b)

Q3. Multiply and reduce to lowest form and convert into a mixed fraction:

Ans:

(i) \( 7\times \frac{3}{5} = \frac{21}{5} = 4\frac{1}{5}\) 

(ii) \( 4\times \frac{1}{3} = \frac{4}{3} = 1\frac{1}{3}\)

(iii) \( 2\times \frac{6}{7} = \frac{12}{7} = 1\frac{5}{7}\)

(iv) \( 5\times \frac{2}{9} = \frac{10}{9} = 1\frac{1}{9}\)

(v) \( \frac{2}{3}\times 4 = \frac{8}{3} = 2\frac{2}{3}\)

(vi) \( \frac{5}{2}\times 6\) =5 x 3 = 15

(vii) \( 11\times \frac{4}{7} = \frac{44}{7} = 6\frac{2}{7}\)

(viii) \( 20\times \frac{4}{5}\) =4 x 4 =16

(ix) \( 13\times \frac{1}{3} = \frac{13}{3} = 4\frac{1}{3}\)

(x) \( 15\times \frac{3}{5}\) = 3 x 3 = 9

Q4. Shade:

Ans: 

Q5. Find:

Ans:

(a) (i) \(\frac{1}{2}\) of 24 = \(\frac{1}{2}\) x 24 = 12

     (ii) \(\frac{1}{2}\) of 46 = \(\frac{1}{2}\) x 46 = 23

(b) (i) \(\frac{2}{3}\) of 18 =  \(\frac{2}{3}\) x 18 = 12

      (ii) \(\frac{2}{3}\) of 27 =  \(\frac{2}{3}\) x 27 = 18

(c) (i) \(\frac{3}{4}\) of 16 = \(\frac{3}{4}\) x 16 = 12

      (ii) \(\frac{3}{4}\) of 36 = \(\frac{3}{4}\) x 36 = 27

(d) (i) \(\frac{4}{5}\) of 20 = \(\frac{4}{5}\) x 20 = 16

      (ii) \(\frac{4}{5}\) of 35 = \(\frac{4}{5}\) x 35 = 28

Q6. Multiply and express as a mixed fraction:

Ans:

(a) 3 x \(5\frac{1}{5}\)

      = 3 x \(\frac{26}{5}\)  

      = \(\frac{78}{5}\) = \(15\frac{3}{5}\)

(b) 5 x \(6\frac{3}{4}\)

      = 5 x \(\frac{27}{4}\)  

      = \(\frac{135}{4}\) = \(33\frac{3}{4}\)

(c) 7 x \(2\frac{1}{4}\)

      = 7 x \(\frac{9}{4}\)  

      = \(\frac{63}{4}\) = \(15\frac{3}{4}\)

(d) 4 x \(6\frac{1}{3}\)

      = 4 x \(\frac{19}{3}\)  

      = \(\frac{76}{3}\) = \(25\frac{1}{3}\)

(e) \(3\frac{1}{4}\) x 6

      = \(\frac{13}{4}\) x 6 

      = \(\frac{78}{4}\) = \(19\frac{1}{2}\)

(f) \(3\frac{2}{5}\) x 8

      = \(\frac{17}{5}\) x 8

      = \(\frac{136}{5}\) = \(27\frac{1}{2}\)

Q7. Find:

Ans:

(a) (i) \(\frac{1}{2}\) of \(2\frac{3}{4}\)

         = \(\frac{1}{2}\) x \(\frac{11}{4}\)

         = \(\frac{11}{8}\) = \(1\frac{3}{8}\)

    (ii) \(\frac{1}{2}\) of \(4\frac{2}{9}\)

         = \(\frac{1}{2}\) x \(\frac{38}{9}\)

         = \(\frac{38}{18}\) = \(2\frac{1}{9}\)

(b) (i) \(\frac{5}{8}\) of \(3\frac{5}{6}\)

         = \(\frac{5}{8}\)x \(\frac{23}{6}\)

         = \(\frac{115}{48}\) = \(2\frac{19}{48}\)

    (ii) \(\frac{5}{8}\) of \(9\frac{2}{3}\)

         = \(\frac{5}{8}\) x \(\frac{29}{3}\)

         = \(\frac{145}{24}\) = \(6\frac{1}{24}\)

Q8. Vidya and Pratap went for a picnic. Their mother gave them a water bottle that contained 5 litres of water. Vidya consumed 2/5 of the water. Pratap consumed the remaining water.
        (i) How much water did Vidya drink?
        (ii) What fraction of the total quantity of water did Pratap drink?

Ans:

Given: Total water= 5 litres

Water consumed by Vidya = 5 x \(\frac{2}{5}\)

                                          = 2 litres

Water consumed by Pratap = 5 - 2 = 3 litres

Fraction of water consumed by Pratap = Water consumed by Pratap / Total water

       = \(\frac{3}{5}\)

Solutions to Ex. 2.2:

Q1. Find:

Ans:

(i) (a) \(\frac{1}{4}\) of \(\frac{1}{4}\)

 = \(\frac{1}{4}\) x \(\frac{1}{4}\)

 = \(\frac{1}{16}\)

    (b) \(\frac{1}{4}\) of \(\frac{3}{5}\)

= \(\frac{1}{4}\) x \(\frac{3}{5}\)

= \(\frac{3}{20}\)

    (c) \(\frac{1}{4}\) of \(\frac{4}{3}\) 

= \(\frac{1}{4}\) x \(\frac{4}{3}\)

= \(\frac{1}{3}\)

(ii) (a) \(\frac{1}{7}\) of \(\frac{2}{9}\)

= \(\frac{1}{7}\) x \(\frac{2}{9}\)

= \(\frac{2}{63}\)

     (b) \(\frac{1}{7}\) of \(\frac{6}{5}\)

= \(\frac{1}{7}\) x \(\frac{6}{5}\)

= \(\frac{6}{35}\)

     (c) \(\frac{1}{7}\) of \(\frac{3}{10}\)

= \(\frac{1}{7}\) x \(\frac{3}{10}\)

= \(\frac{3}{70}\)

Q2. Multiply and reduce to lowest form (if possible) :

Ans:

(i) \(\frac{2}{3}\) x \(2\frac{2}{3}\)

    = \(\frac{2}{3}\) x \(\frac{8}{3}\)

    = \(\frac{16}{9}\) = \(1\frac{7}{9}\)

(ii) \(\frac{2}{7}\) x \(\frac{7}{9}\)

    = \(\frac{2}{9}\)

(cancelling 7 from the numerator & denominator)

(iii) \(\frac{3}{8}\) x  \(\frac{6}{4}\)

    = \(\frac{3}{8}\) x  \(\frac{3}{2}\)

    = \(\frac{9}{16}\)

(iv) \(\frac{9}{5}\) x  \(\frac{3}{5}\) = \(\frac{27}{25}\)

    = \(1\frac{2}{25}\)

(v) \(\frac{1}{3}\) x  \(\frac{15}{8}\)

     = \(\frac{5}{8}\)

(As 15 in numerator is ÷ 3 in denominator to give 5)​

(vi) \(\frac{11}{2}\) x  \(\frac{3}{10}\)

      = \(\frac{33}{20}\)

      = \(1\frac{13}{20}\)

(vii) \(\frac{4}{5}\) x \(\frac{12}{7}\)

      = \(\frac{48}{35}\)

      = \(1\frac{13}{35}\)

Steps: 

1. Check the numerator & denominator for numbers that can be reduced.
2. When nothing can be simplified, multiply the numerator with numerator & denominator with denominator.
3. Convert the final answer to mixed fraction.

Q3. Multiply the following fractions:

Ans:

(i) \(\frac{2}{5}\times \ 5\frac{1}{4}\)

\(\frac{2}{5}\) x \(5\frac{1}{4}\)

     = \(\frac{2}{5}\) x \(\frac{21}{4}\) 

     = \(\frac{21}{10}\) = \(2\frac{1}{10}\)

(ii) \(6\frac{2}{5}\) x \(\frac{7}{9}\)

      = \(\frac{32}{5}\) x \(\frac{7}{9}\)

      = \(\frac{224}{45}\) = \(4\frac{44}{45}\)

(iii) \(\frac{3}{2}\) x \(5\frac{1}{3}\)

      = \(\frac{3}{2}\) x \(\frac{16}{3}\) 

      = 8

(iv) \(\frac{5}{6}\) x \(2\frac{3}{7}\)

      = \(\frac{5}{6}\) x \(\frac{17}{7}\)

      = \(\frac{85}{42}\) = \(2\frac{1}{42}\)

(v) \(3\frac{2}{5} \times \frac{4}{7}\)

       =\(\frac{17}{2} \times \frac{4}{7}\)

       = \(\frac{68}{35}\) = \(1\frac{33}{35}\)

(vi) \(2\frac{3}{5}\) x 3

       =\(\frac{13}{5}\) x 3

       = \(\frac{39}{5}\) = \(7\frac{4}{5}\)

(vii) \(3\frac{4}{7} \times \frac{3}{5}\)

       =\(\frac{25}{7} \times \frac{3}{5}\)

       = \(\frac{75}{35}\) = \(2\frac{1}{7}\)

Q4.Which is greater:

Ans:

(i) \(\frac{2}{7}\) of \(\frac{3}{4}\)

     =  \(\frac{2}{7}\) x \(\frac{3}{4}\)

     = \(\frac{3}{14}\)

   \(\frac{3}{5}\) of \(\frac{5}{8}\)

    = \(\frac{3}{5}\) x \(\frac{5}{8}\)

   = \(\frac{3}{8}\)

To compare \(\frac{3}{14}\) & \(\frac{3}{8}\)

LCM 0f 14 & 8 is 56

Hence,

\(\frac{3}{14}\) = \(\frac{12}{56}\) &

\(\frac{3}{8}\) = \(\frac{21}{56}\)

Comparing numerators

12 < 21

\(\frac{3}{5}\) of \(\frac{5}{8}\) is greater.

(ii) \(\frac{1}{2}\) of \(\frac{6}{7}\)

     = \(\frac{1}{2}\) x \(\frac{6}{7}\)

     = \(\frac{6}{14}\) = \(\frac{3}{7}\)

    \(\frac{2}{3}\) of \(\frac{3}{7}\)

    = \(\frac{2}{3}\) x \(\frac{3}{7}\)

    = \(\frac{2}{7}\)

As denominators are same, comparing numerators

3 > 2

\(\frac{1}{2}\) of \(\frac{6}{7}\) is greater.

Q5. Saili plants 4 saplings, in a row, in her garden. The distance between two adjacent saplings is 3/4 m. Find the distance between the first and the last sapling.

Ans:

Given: Number of saplings in a row = 4

            Distance between each sapling = \(\frac{3}{4}\)m

Distance between first & last sapling

= 3 x \(\frac{3}{4}\)

= \(\frac{9}{4}\) = \(2\frac{1}{4}\)m

Q6. Lipika reads a book for \(1\frac{3}{4}\) hours everyday. She reads the entire book in 6 days. How many hours in all were required by her to read the book?

Ans:

Given: Time per day = \(1\frac{3}{4}\) = \(\frac{7}{4}\) hrs.

   Number of days = 6

Total hours = 6 x \(\frac{7}{4}\)

= \(\frac{21}{2}\)

= \(10\frac{1}{2}\) hours

Q7. A car runs 16 km using 1 litre of petrol. How much distance will it cover using \(2\frac{3}{4}\) litres of petrol.

Ans:

Given: Distance in 1 litre petrol= 16km

Distance covered = \(2\frac{3}{4}\) x 16

 = \(\frac{11}{4}\) x 16

 = 44 km

Q8. Ans:

(a)  (i) 5/10

      (ii) 1/2

(b) (i) 8/15

     (ii) 8/15

Solutions to Ex. 2.3

Q1. Find:

Ans:

(i) 12 ÷ \(\frac{3}{4}\)

    = 12 x \(\frac{4}{3}\) = 16

(ii) 14 ÷ \(\frac{5}{6}\)

     = 14 x \(\frac{6}{5}\)

     = \(\frac{84}{5}\) = \(16\frac{4}{5}\)

(iii) 8 ÷ \(\frac{7}{3}\)

     = 8 x \(\frac{3}{7}\)

     = \(\frac{24}{7}\) = \(3\frac{3}{7}\)

(iv) 4 ÷ \(\frac{8}{3}\)

     = 4 x \(\frac{3}{8}\)

     =  \(\frac{3}{2}\) 

(v) 3 ÷ \(2\frac{1}{3}\) = 3 ÷ \(\frac{7}{3}\)

     = 3 x \(\frac{3}{7}\)

     = \(\frac{9}{7}\) = \(1\frac{2}{7}\)

(vi) 5 ÷ \(3\frac{4}{7}\) = 5 ÷ \(\frac{25}{7}\)

     = 5 x \(\frac{7}{25}\) = \(\frac{7}{5}\)

Q2. Find the reciprocal of each of the following fractions. Classify the reciprocals as proper fractions, improper fractions and whole numbers.

Ans: Reciprocals are:

(i) \(\frac{7}{3}\), Improper fraction.

(ii) \(\frac{8}{5}\), Improper fraction.

(iii) \(\frac{7}{9}\), Proper fraction.

(iv) \(\frac{5}{6}\), Proper fraction.

(v) \(\frac{7}{12}\), Proper fraction.

(vi) 8, Whole number.

(vii) 11, Whole number.

Q3. Find:

Ans:

(i) \(\frac{7}{3}\) ÷ 2

     = \(\frac{7}{3}\) x \(\frac{1}{2}\)

     = \(\frac{7}{6}\) = \(1\frac{1}{6}\)

(ii) \(\frac{4}{9}\) ÷ 5

     = \(\frac{4}{9}\) x \(\frac{1}{5}\)

     = \(\frac{4}{45}\)  

(iii) \(\frac{6}{13}\) ÷7

      = \(\frac{6}{13}\) x \(\frac{1}{7}\)

      = \(\frac{6}{91}\)

(iv) \(4\frac{1}{3}\) ÷ 3

      = \(\frac{13}{3}\) x \(\frac{1}{3}\)

      = \(\frac{13}{9}\) = \(1\frac{4}{9}\)

(v) \(3\frac{1}{2}\) ÷ 4

      = \(\frac{7}{2}\) x \(\frac{1}{4}\)

      =\(\frac{7}{8}\)

(vi) \(4\frac{3}{7}\) ÷ 7

      = \(\frac{31}{7}\) x \(\frac{1}{7}\)

      = \(\frac{31}{49}\)

Q4. Find:

Ans:

(i) \(\frac{2}{5}\) ÷ \(\frac{1}{2}\)

     = \(\frac{2}{5}\) x 2 =  \(\frac{4}{5}\)

(ii) \(\frac{4}{9}\) ÷\(\frac{2}{3}\)

     =  \(\frac{4}{9}\) x \(\frac{3}{2}\) = \(\frac{2}{3}\)

(iii) \(\frac{3}{7}\) ÷ \(\frac{8}{7}\)

      =  \(\frac{3}{7}\) x \(\frac{7}{8}\) =  \(\frac{3}{8}\) 

(iv) \(2\frac{1}{3}\) ÷ \(\frac{3}{5}\)

      = \(\frac{7}{3}\) x \(\frac{5}{3}\)

      = \(\frac{35}{9}\) = \(3\frac{8}{9}\)

(v) \(3\frac{1}{2}\) ÷ \(\frac{8}{3}\)

     = \(\frac{7}{2}\) x \(\frac{3}{8}\)

     = \(\frac{21}{16}\) =\(1\frac{5}{16}\)

(vi) \(\frac{2}{5}\) ÷ \(1\frac{1}{2}\)

     = \(\frac{2}{5}\)÷ \(\frac{3}{2}\) 

     = \(\frac{2}{5}\) x \(\frac{2}{3}\) = \(\frac{4}{15}\) 

(vii) \(3\frac{1}{5}\) ÷ \(1\frac{2}{3}\)

     = \(\frac{16}{5}\)÷ \(\frac{5}{3}\) 

     = \(\frac{16}{5}\) x \(\frac{3}{5}\)

     = \(\frac{48}{25}\) = \(1\frac{23}{25}\)

(viii) \(2\frac{1}{5}\) ÷ \(1\frac{1}{5}\)

     = \(\frac{11}{5}\)÷ \(\frac{6}{5}\) 

     = \(\frac{11}{5}\) x \(\frac{5}{6}\)

     = \(\frac{11}{6}\) = \(1\frac{5}{6}\)